Erddruck auf Winkelstützwände

Leitung: Prof. Dr.-Ing. Martin Achmus
Bearbeiter: Prof. Dr.-Ing. Martin Achmus
Laufzeit: Abschluss 2006   

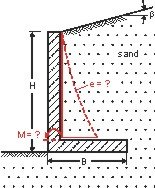
Die Bemessung des vertikalen Schenkels von Winkelstützwänden ist gemäß derzeitiger deutscher Normung für erhöhten Erddruck, d. h. den Mittelwert aus aktivem Erddruck und Erdruhedruck vorzunehmen. Dieser Ansatz liegt in vielen Fällen deutlich auf der sicheren Seite. Wegen des Vorhandenseins des horizontalen Sporns ist zwar davon auszugehen, dass im unteren Wandbereich ein höherer als der aktive Erddruck wirkt. Dies muss jedoch nicht für den oberen Bereich gelten.

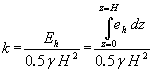
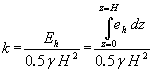
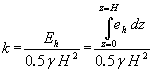
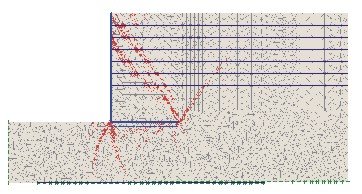
Mit einem numerischen Modell kann der Erddruck auf den vertikalen Sporn berechnet werden. Das verwendete Finite Elemente-Netz ist für ein Beispiel in Abbildung 2 wiedergegeben. Es wurde eine sehr feine Diskretisierung gewählt, um eine genaue Auflösung des Wandspannungsverlaufs zu erhalten. Markiert sind in Bild 2 auch die Bereiche, in denen sich - beispielhaft für den Fall der mitteldichten Lagerung des Bodenmaterials - die größten Dehnungsinkremente ergeben. Deutlich erkennt man hier die zu erwartende Ausbildung zweier, vom Ende des Wandsporns ausgehender und nach oben verlaufender Gleitfugen. In der Berechnung wurde zunächst für den Untergrund ein verformungsfreier Initialspannungszustand generiert. Anschließend wurden die Wandherstellung und die Hinterfüllung simuliert. Für letztere wurde dabei die Aufbringung in einzelnen Lagen von 1 m Dicke simuliert. Ergebnisse sind in Abbildung 3 dargestellt.

.

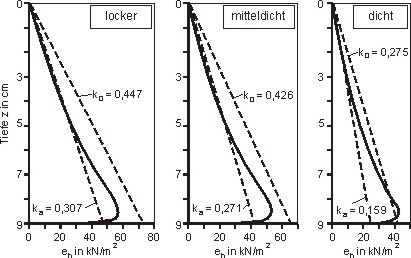
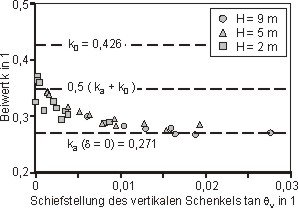
Es zeigte sich, dass der Erddruckbeiwert k vereinfacht abhängig von der mittleren Schiefstellung des vertikalen Wandschenkels θ_v gewählt werden kann (Abbildung 4).

Daraus ergibt sich eine einfache Vorgehensweise zur genaueren Bestimmung des Erddrucks auf den vertikalen Schenkel in der Praxis:

• Ermittlung der Setzungen und damit der "Starrkörper"-Schiefstellung der Winkelstützwand durch herkömmliche Berechnung einer durch aktiven Erddruck belasteten Ersatzschwergewichtswand
• Berechnung der zusätzlichen mittleren Schiefstellung des vertikalen Wandschenkels infolge Biegeverformung durch Erddruck. Vereinfacht kann dabei ebenfalls aktiver Erddruck angesetzt werden.
• Berechnung der zusätzlichen mittleren Schiefstellung des vertikalen Wandschenkels infolge Biegeverformung durch Erddruck. Vereinfacht kann dabei ebenfalls aktiver Erddruck angesetzt werden.
• Der in Abbildung 4 dargestellte, rechnerisch ermittelte Zusammenhang bedarf noch der experimentellen Verifikation. Mit dem hier vorgestellten Ansatz wird aber ein zweckmäßiger und praktikabler Weg für die zukünftig wünschenswerte genauere Ermittlung des Erddrucks auf den vertikalen Wandschenkel aufgezeigt.

[1] Achmus, M., Rouili, A. (2004). Untersuchung zur Erddruckbeanspruchung von Winkelstützwänden. Bautechnik Heft 12, Dezember 2004, 81. Jg., S. 942-948.

[2] Achmus, M. (2006). Numerical modelling on earth pressure loading of the vertical stem of L-shaped retaining walls. 6th European Conference on Numerical Methods in Geotechnical Engineering, Graz, Sept. 2006.